한글이 과학적이라는 사실은 공공연하게 언급할 필요도 없는 사실이다. 하지만 ‘한글이 왜 과학적이죠?’라고 누군가 묻게 된다면 쉽게 그 이유를 말할 수 없는 것이 사실이다. 필자 역시 한글이 왜 과학적인지에 대한 물음을 가지고 있었고 마침 「한글과 언어문화」라는 수업을 통해 스스로 조사할 수 있는 기회를 가지게 되었다. 우선 한글의 과학성에 대한 얘기를 하기에 앞서 이 글에서는 한국어를 표기하는 문자인 한글의 과학성을 따질 것이지 한국어의 과학성을 따지지는 않을 것이다.
I. 과학적이란?
한글의 과학성을 따지기 위해서는 ‘과학적’이라는 말의 의미를 먼저 파악하고 넘어가는 것이 좋겠다. ‘과학적’의 사전적인 의미는 ‘사실 그 자체로 뒷받침되고, 논리적인 인식으로 매개되어 있는 (것). 원리적으로 체계가 세워져 있는 (것)’이다. 간단하게 말해 ‘관찰을 통해 논리적인 인식으로 도달되어진 것’을 말하는데 그렇다면 ‘과학적인 한글’이라는 말은 어떻게 해석해야 할까?
1. ‘과학적인 한글’의 의미
위에서 언급한 ‘과학적’의 의미를 생각해 볼 때, ‘과학적인 한글’의 의미는 무엇일까? 아마도 이는 훈민정음의 다음 구절을 통해 추리해 볼 수 있을 것 같다.
㉠ ‘나라 말이 중국과 달라서 한자와는 서로 통하지 못한다. 그러므로 어리석은 백성들이 말하고 싶은 바가 있어도 마침내 그 뜻을 펴지 못하는 이가 많다. 내가 이것을 매우 딱하게 여기어 새로 스물여덟글자를 만들어 내노니 사람마다 쉽게 익히어 일상생활에 편리하게 쓸 수 있도록 할 따름이니라.’
㉡ ‘이제 훈민정음을 만든 것은 처음부터 지혜로 경영하고 힘써서 찾은 것이 아니요. 다만 그 말소리에 따라 그 이치를 다했을 뿐이다. 이치는 둘이 아닌즉 어찌 천지음양과 더불어 그 쓰임을 같이하지 않을 수 있으랴. 훈민정음 28자는 각각 그 형상을 본떠서 만들었다.’
훈민정음의 구절을 통해 두 가지 방향에서 ‘과학적인 한글’의 의미를 살펴볼 수 있다. 첫째로 ㉠으로부터 한글은 영어와 같이 오랜 역사를 두고 점차로 진화되어온 문자가 아니라 세종대왕과 집현전 학자들에 의해 “발명”된 문자이다. 그리고 둘째로 ㉡로부터 알 수 있듯이 한글은 한자와 같은 뜻글자가 아닌 말소리를 기본으로 하여 만들어진 글자임을 알 수 있다. 이제 위의 ‘과학적’의 의미와 함께 생각해보자. 그리 어렵지 않게 우리의 말소리가 나오는 조음기관을 관찰하고 이를 논리적인 인식으로 분석하여 문자를 만들었음을 생각할 수 있다. 안타깝게도 필자의 지식이 부족하여 조음기관을 얼마나 과학적으로 분석했는지를 설명하기는 어렵다. 그렇다면 한글이 얼마나 폭넓게 말소리를 표현할 수 있는지를 다른 언어와 비교해 살펴봄으로써 한글의 방대한 표현력을 확인해 보고 조음기관이 내는 말소리에 대한 분석이 얼마나 잘 되었는지를 느껴 보도록 하자.
2. 영어와의 비교
한글을 세계 공용어로 쓰이는 영어의 모음과 비교해 보도록 하자. 한글이 말소리 문자인 만큼 같은 소리문자 중 현대에 가장 널리 쓰이는 영어와 비교해 보는 것이 좋을 것 같다. 우선 비교에 앞서 자음 체계에 대해서는 언급하지 않도록 하겠다. 필자 개인적인 생각으로 어떤 음을 발음하는데 있어 모음만으로는 그 글자를 발음할 수 있지만 자음만으로는 그 글자를 발음할 수 없다고 생각되기 때문이다. 예를 들어 ‘ㅈ’을 발음하라고 한다면 대다수는 ‘즈’로 발음할 것이다. 즉 모음 ‘ㅡ’를 첨가하여 읽는 것이다. 하지만 모음의 경우 ‘ㅠ’, ‘ㅗ’는 자음 없이도 ‘유’, ‘오’로 발음할 수 있다. 또 영어의 경우 'a' 하나 만으로도 ‘ㅏ’, ‘ㅐ’, ‘ㅔ’, ‘ㅓ’ 등으로 발음되기 때문에 영어의 모음은 발음 기호를 통해 비교하도록 하겠다.
아래 표는 영어의 모음을 구강 내의 위치에 따라 구분한 도표이다. 표의 왼쪽에 적힌 것이 영어의 모음을 표현한 발음 기호이며 오른쪽이 그것을 표현한 한글이다. 영어와 국어의 발음상의 차이에 의해 한글로 정확히 표현할 수 없는 모음이 있는 것이 사실이나 약간의 수정과 약속을 통해 이를 극복할 수 있으리라 생각된다. 아래의 도표뿐만이 아니라 영어에는 반모음(semivowel)이 있고 또 r 앞에서의 모음의 소리도 구별하는데 이들 역시 한글로 표현이 가능하다. 애초의 목적이 다른 소리 문자를 표현할 수 있음을 보이려는 의도였으므로 반모음의 예만을 보고 지나가자.

영어의 반모음에는 [w]와 [j]가 있다. [w]의 예로는 won, which, question 등이 있는데 한글의 ‘ㅜ’와 유사한 기
능을 한다. 그리고 [j]의 예로는 yet, bullion, cañon 등이 있으며 이는 ‘ㅣ’와 유사한 기능을 하고 있음을 볼 수
있다. 한 가지 특이한 점은 ‘우’와 ‘이’는 이미 언급되었던 모음이라는 것이다. 하지만 반모음에서의 [j]와 [w]는
‘우이(위)’, ‘우어(워)’, ‘이어(여)’, ‘이에(예)’ 등의 모음 간의 결합 형태일 경우에 쓰임을 알 수 있다. 필자와 생각
을 같이 하는 독자라면 아마 이 쯤에서 한글이 영어 문자 뿐만 아니라 발음 기호에 비교해서도 보다 경제적이고
과학적이 아닌가라는 생각을 할 수도 있으리라.
위에서 볼 수 있었듯이 한국어가 아닌 영어의 모음 기관을 한글이 표현할 수 있음을 보았다. 그렇다면 한글이 표현할 수 있는 모음은 영어 알파벳으로 표현할 수 있을까? 대답은 매우 간단한 것 같다. 단적인 예로 ‘ㅓ’가 쓰이는 단어는 영어 알파벳으로 표현하기 매우 어려움을 알 수 있다. 예를 들어 ‘거울’을 ‘Geowool’로 적을 경우 ‘게오울’ 혹은 ‘지오울’등으로 발음이 가능하며 ‘서서히’의 경우 역시 ‘Seoseohee’라고 적어야 할지 ‘Susuhee’라고 적어야 할지 알 수 없다.
위의 비교를 통해 영어의 모음 소리를 한글이 매우 근접한 위치까지 표현할 수 있으며 영어 알파벳은 한글이 표현하는 모음 소리를 정확히 표현하지 못함을 보았다. 이를 통해 우리는 한글이 세계에서 가장 널리 쓰이는 말소리 문자(영어) 보다 폭 넓은 표현력을 가졌음을 알 수 있었으며 이는 곧 우리 조음기관이 내는 소리를 한글이 얼마나 잘 포착하고 있는지를 좁게나마 알 수 있게 해준다. 한글이 우리의 조음기간이 내는 소리를 잘 포착함을 보여주는 위의 예만으로도 한글이 얼마나 과학적인가를 생각할 수 있을 듯하다. 이쯤에서 위의 ‘과학적’이라는 말의 의미를 다시 한 번 상기시켜 보자. ‘과학적임’은 사실 그 자체로 뒷받침된다는 관찰의 특징 외에 ‘논리적인 인식으로 매개되어 있는 그리고 원리적으로 체계가 세워져 있는 것’이라고 했다. 한글이 과학적이라면 이는 논리적인 인식을 매개로 체계를 지니고 있다는 해석이 가능하다. 체계성을 지니고 있다는 것은 유한한 규칙에 의해 일관적으로 작용된다는 의미이며 이는 “규칙화 가능” 즉, 실용성을 담지하고 있다는 해석이 가능하다. 이제 한글이 현대 사회에 얼마나 실용적으로 사용될 수 있는지 혹은 얼마나 잘 만들어진 체계인지 살펴보도록 하자.
II. 한글의 체계성과 실용성
위에서 한글의 체계성과 실용성의 연결 관계를 개괄적으로 언급했다. 이번 장에서는 일반적으로 잘 알려진 언어의 사용의 측면에서 한글이 얼마나 이해하기 편하게 만들어져 있는지를 살펴보고 수학의 공리론적인 체계에 부합하는 한글의 모습을 통해서 컴퓨터 프로그래밍 및 과학 분야에 적용 가능성을 살펴보겠다. 그리고 마지막으로 컴퓨터에 적용된 한글 사용의 몇 가지 사례 및 과학자들이 말하는 한글의 가능성에 대한 자료를 통해 한글의 과학성을 보다 뒷받침하도록 하겠다.
1. 언어 사용으로 바라보는 실용성
⑴ 가획의 원리
한글의 글자는 기본적으로 가획의 원리를 가지고 있다. ‘가획의 원리’란 ‘ㄱ, ㄴ, ㅁ, ㅅ, ㅇ’와 같은 초성이라 불리는 기호에 획을 하나씩 더하여 글자가 만들어지는 원리라는 말이다. 그리고 이는 훈민정음에 매우 자세히 설명되어 있다.
‘ㄱ는 혀뿌리가 목구멍을 막는 현상을 본뜬 것이요. 혓소리 ㄴ은 입의 형상을 위 잇몸에 닿는 형상을 본뜬 것이요. 입술소리 ㅁ은 입의 형상을 본뜬 것이요. 잇소리 ㅅ은 이의 형상을 본뜬 것이요. 목구멍소리 ㅇ은 목구멍의 형상을 본뜬 것이다. ㅋ은 ㄱ보다 소리가 좀 거세게 나는고로 획을 더한 것이니 ㄴ에서 ㄷ, ㄷ에서 ㅌ, ㅁ에서 ㅂ, ㅂ에서 ㅍ, ㅅ에서 ㅈ, ㅈ에서 ㅊ, ㅇ에서 ㆆ, ㆆ에서 그 소리에 따라 획을 더한 뜻은 다 같다. 그러나 오직 ㅇ 만은 다르게 하고 반혀소리 ㄹ와 반잇소리 △도 역시 혀와 이의 모양을 본떴으나 그 모양을 다르게 하였을 뿐 획을 더한 뜻은 없다.’
아래의 표는 훈민정음에 적힌 초성체계를 분류한 표이다. 그리고 옆은 한글 글자와 음이 유사한 영어의 문자이다. 이 표를 통해서도 알 수 있듯이 한글의 기본이 되는 글자(기본자)와 획을 더한 글자(가획자)간의 구조가 소리를 내는 혀의 위치와 입술의 작용에 매우 잘 부합함을 알 수 있다. 그에 반해 옆의 영어를 보도록 하자. 영어에도 역시 자음과 모음간의 구별이 있기는 하나 글자 표기에 있어 연관성이 없다. 기본자에 한 획을 더한 글자가 같은 방식으로 소리를 내는 문자가 되는 한글에 비해 영어는 연관성 없는 글자들 간의 나열이 된다. 즉 문자를 배우고 사용하는데 있어 영어가 훨씬 어려움이 많은 것이다.

⑵ 자질 문자로서의 한글의 특징
영국 리즈대학 음성언어학과 제프리 샘슨(Geoffrey Sampson) 교수는 ‘문자 체계(Writing System, 1985)’에서 세계의 문자를 분류하는데 그는 “문자는 표의문자에서 표음문자로, 표음문자는 다시 음절문자에서 음소문자의 형태로 발전한다”고 주장했다. 이 분류에 따르면 한자는 대표적인 표의문자이고 일본 문자인 가나는 표음문자 중에서도 음절문자에 해당한다. 그리고 영어는 음소문자로 분류될 수 있다. 샘슨 교수는 한글에 대해 ‘자질(feature)문자’라고 분류하는데 그는 “한글은 과학적으로 볼 때 의심할 여지없이 세계에서 가장 훌륭한 글자”라며 한글만을 위해 ‘자질문자’라는 조항을 새로 만들었다고 한다.<제프리 샘슨 문자체계 참조>

이렇게 자질문자로 분류되는 한글은 영어와 같이 음소 단위의 글자를 사용하면서도 이를 음절 단위로 배열한다. ‘음소’란 ‘더 이상 더 작은 음운적 단위로 나눌 수 없는 최소 단위’이며 하나 이상의 음소가 모여 음절을 이룬다. ‘음절’이란 ‘하나의 종합된 음의 느낌을 주는 단어의 구성 요소로서의 음의 단위’이며 우리가 실제 말하고 청취할 수 있는 음성의 최소 단위라고 한다. 그렇다면 같은 음소 단위를 사용하는 영어 단어에서 음절을 파악해 보자. 아래 표는 각 영어 단어에 따른 음절수를 정리한 것이다.

가장 왼쪽의 ‘furniture’, ‘impossible’, ‘remember’의 경우는 ‘퍼니쳐’, ‘임파서블’, ‘리멤버’로 쉽게 그 음절의 수를 파악할 수 있다. 하지만 오른쪽의 단어들을 보자. ‘examination’의 경우 ‘이그제머네이션’으로 읽어지며 음절의 수가 7개인 것 같지만 ‘익-제-머-네-이-션’으로 음절수가 5개가 된다. 마지막의 ‘brought’를 보자. 우리는 쉽게 ‘브로우트’라고 생각해 4개의 음절을 가진다고 할지 모르나 ‘ㅂ롯’으로 한 개의 음절을 가진다. 그렇다면 한글은 어떨까?
다음의 음절수는 몇 개인가? ‘한글’, ‘고려대학교’, ‘한글과 언어문화’. 아마도 이러한 단어의 음절수를 묻는 질문에 독자는 매우 당황스러울 것이다. 왜냐하면 너무도 당연한 것을 묻는 것이기 때문이다. ‘한글’의 음절수는 2개이며 ‘고려대학교’의 음절수는 5, ‘한글과 언어문화’의 음절수는 7이다. 이렇게 한글은 음절수와 글자수가 일치된다. 앞서 얘기했듯이 음소단위의 글자를 사용하면서 음절단위로 나누어져있기 때문에 음절을 파악하는데 매우 용이하다. 특히나 음절이 ‘우리가 실제 말하고 청취할 수 있는 음성의 최소 단위’라는 측면에서 글을 이해하고 사용하는데 매우 용이하다.
지금까지 한글의 가획의 원리와 자질문자로서의 특징을 알아보았다. 이 두 가지만을 통해서도 우리는 한글이 적은 수의 기본 글자를 통해 다양한 음성을 표현할 수 있으며 언어 교육에 있어서도 지각적으로 쉽게 인식할 수 있는 장점이 있음을 보았다. 그렇다면 이 한글을 컴퓨터 프로그램으로 혹은 다른 응용과학 분야에 사용한다면 어떨까? 이제 언어학의 측면이 아닌 수학의 측면에서 한글의 체계성을 살펴보도록 하자.
2. 공리 체계(컴퓨터 프로그래밍)의 측면에서 바라본 한글의 실용성
현대의 많은 학문 중에 가장 체계적인 학문을 꼽으라면 사람들은 단연 수학을 꼽을 것이다. 그리고 이 수학 체계는 공리(Axiom)이라고 하는 수학자들 사이의 약속에 의해 그 구조물이 세워져 있다. 이 글에서 수학의 공리체계에 대한 상세한 설명은 접어두도록 하겠다. 이 글의 주제와는 상당히 동떨어져있기 때문이다. 그리고 수학에 익숙하지 않은 사람들의 편의를 위해 ‘공리’라는 말 대신 ‘규칙(rule)’이라는 말로 이를 대신하도록 하겠으며 ‘규칙’이라는 용어 사용을 통해 일어나는 오해에 대해서는 양해를 구한다.
⑴ 수학의 공리 체계
한글의 체계성을 말하면서 수학을 얘기하는데 대해 매우 의아하게 생각하는 사람들도 있으리라 생각된다. 하지만 20세기 초, 완전한 수학의 체계를 설립하려는 수학자들의 노력에 의해 세워진 공리체계는 현대 컴퓨터이론의 토대가 된다. 현대에는 수학을 기본적으로 10가지의 ‘공리(Axiom)’라 불리는 규칙으로 이루어진 체계로 해석하는데 이해하기 어렵다면 일종의 컴퓨터 프로그램으로 생각하면 되겠다. 각기 다른 프로그램을 작동시키고 새로운 프로그램을 만드는 기초가 되는 규칙이 ‘공리’이다. 유명한 페르마의 정리 역시 이 공리로부터 도출될 수 있으며 이러한 측면에서 수학자들이 하는 일은 어떠한 수학적 사실이 공리로부터 도출 가능한 ‘정리(Theorem)’인지 아닌지를 밝혀내는 것이라 하겠다. 그렇다면 이 규칙체계(공리체계)가 한글의 실용성과 어떠한 관계가 있을까?
바둑을 예로 들어 보자. 아래는 필자가 임으로 바둑에 대한 기본 규칙을 생각해본 것이다.
① 361(=19×19)개의 움직일 수 있는 길이 있다.
② 흑돌과 백돌만을 사용할 수 있다.
③ 한 번에 한 자리에만 돌을 놓을 수 있으며 한 사람은 한 가지 돌만을 사용할 수 있다.
④ 한 사람이 연속으로 두 번 돌을 놓을 수 없다.
⑤ 한 돌을 다른 돌이 빈 공간 없이 둘러싸면 둘러싼 돌의 주인이 이 돌을 가진다.
⑥ 한쪽이 기권하거나 더 이상 놓을 수 없을 때까지 돌을 놓는다.
⑦ 돌로 둘러싼 공간이 많은 쪽이 이긴다. (상대방의 돌을 가지고 있는 만큼 상대방의 공간을 채울 수 있다.)
현대에도 바둑은 일종의 신선놀음으로 불릴 정도로 그 수가 매우 다양하며 두뇌 게임의 최고봉에 달해 있을 정도로 그 전문성을 인정받는 게임이다. 하지만 이렇게 복잡한 바둑도 위의 7가지 정도의 규칙으로 이루어져있음을 알 수 있다. 몇 천 몇 만 가지의 수가 단 7가지의 규칙에 기초해 있는 것이다. 하지만 바둑의 ‘수’라고 불리는 바둑의 전략을 표현하기에는 7가지 규칙으로는 어려운 점이 많다. 전략 표현을 위해 더욱 많은 규칙을 추가할 수가 있으며 규칙의 추가를 통해 다양한 측면의 규칙을 보다 손쉽게 표현할 수 있다. 말하자면 덧셈만을 가지고 셈을 하는 것 보다 곱셈 체계가 더해졌을 경우 큰 수에 대한 계산이 훨씬 빨라지는 이치다. 이렇게 규칙은 많을수록 복잡한 표현이 보다 손쉽게 이루어진다. 하지만 문제는 규칙이 많을수록 그 체계가 오류를 일으킬 가능성이 높아진다. 오류를 줄이기 위해서는 추가하는 규칙이 오류를 일으키지 않는다는 보장이 있어야 하는데 체계를 만드는 과정에서 그러한 검증 과정을 가지기 힘들다. 컴퓨터 프로그램도 마찬가지다. 규칙이 많으면 많을수록 시스템이 오류를 가질 확률이 높아진다. 반면에 규칙을 줄이면 줄일수록 어떠한 결과를 이끌어내는 과정(process)이 오래 걸린다. 그래서 오류를 최소화하면서 가장 빠른 효율적인 방향을 찾기 위해 노력해야 하는 것이다. 지금까지 수학적 체계 즉, 컴퓨터 프로그램의 기본적인 체계를 알아보았다. 그렇다면 이제 한글을 컴퓨터에 구현한다고 했을 때, 한글에 대한 규칙이 어떻게 이루어질 수 있고 이것이 어떠한 체계성 그리고 효율성을 가지는지 알아보도록 하자.
⑵ 암호화(Coding) 과정을 통한 한글의 경제성 비교
앞서 우리는 한글이 초성자를 기본으로 가획의 원리를 통해 이루어졌음을 알았다. 그리고 이 가획의 원리를 앞장의 규칙에 대한 설명에 대응시킨다면 한글이 충분히 수학적 규칙성의 체계(수학적 공리 체계)를 가질 수 있음을 예측할 수 있을 것이다. 이제 지금까지의 지식을 바탕으로 한글의 글자를 컴퓨터에 인식시키는 방법을 임의로 구성해 보도록 하겠다. 그리고 이 방법을 영어에도 적용해 봄으로써 영어에 비해 한글이 가지는 체계성 및 경제성을 알아볼 것이다.
기본적인 아이디어는 유클리드 기하학의 점과 선 그리고 원에 대한 공리와 함께 가획의 원리를 응용할 것이다. 모든 도형의 기본은 “점”이므로 점으로부터 선과 원을 정의할 수 있다. 다음은 필자가 임의로 구성한 점, 선, 그리고 원의 규정이다.
임의의 평면 A = {<x, y>∈ $R^2$ ∣ 0 ≤ x ≤ 3, 0 ≤ y ≤ 3}에 대해,
규칙 1> 주어진 임의의 평면A에 대해 하나 이상의 점이 있다.
정의 1> 어떤 두 점 A, B가 있다면 A와 B를 포함하며 이들 사이를 빈 공간 없이 채운 점들의 집합을 점 AB를 잇는 ‘선’이라고 한다.
정의 2> 어떤 점 A와 같은 거리에 있는 모든 점들의 집합을 ‘원’이라고 한다.
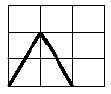
위의 정의에 따라 아래 그림의 가장 굵은 선은 $\overline{AB}$ = {<x, y>∈ $R^2$ ∣ 0 ≤ x ≤ 1, y = 3}와 같이 점들의 집합으로 표현될 수 있다.

ㅅ을 표현하기 위한 두 대각선 역시 $\overline{CD} = \{ <x,y> \in R^2 | y=2x \wedge 0 \leq x \leq 1, 0 \leq y \leq 2 \}$와 $\overline{EF} = \{ <x,y> \in R^2 | y=-2x+3 \wedge 0 \leq x \leq 1, 0 \leq y \leq 2 \}$와 같이 점들의 집합으로 표현될 수 있다. 그리고 ㅅ은 $\overline{CD} \cup \overline{EF}$로 표현할 수 있다.
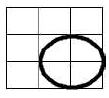
마찬가지로 원 역시 $\widehat{G} = \{ <x,y> \in R^2 | (x-2)^2 + (y-1)^2 = 1 \wedge 1 \leq x \leq 2, 1 \leq y \leq 2 \}$와 같이 점들의 집합으로 표현될 수 있다.
이제 다음 규칙으로 넘어가자.
규칙 2> 모든 선의 집합은 x, y 둘 중 하나의 좌표가 꼭 $n \leq 3$과 같아야 하며 나머지 좌표의 범위의 크기는 1을 넘어서는 안 된다.
규칙 3> ㅅ의 집합은 규칙 2에 예외로 한다.
규칙 4> 유일한 원의 집합 $\widehat{G}$가 존재한다.
이렇게 규칙 2, 3, 4를 통해서 \overline{AB}$와 같은 24개의 선의 집합과 ㅅ의 집합 그리고 $\widehat{G}$의 원의 집합으로 이루어진 도형들의 집합이 구성된다. 그리고 이들을 이용해 아래와 같은 한글의 기본 글자들이 표현된다.

이제 남은 작업은 이들을 컴퓨터에 인식 시키는 작업이다. 컴퓨터는 기본적으로 2진법으로 프로그램이 구성된다.
복잡한 설명은 생략하고 본론만을 말한다면 위에서 구성한 선, 대각선 그리고 원에 특정수를 부여하고 이를 2진
법으로 고친 후 회로를 구성하면 된다. 본격적인 암호화(coding)작업은 생략하고 공리를 하나 더 추가하여 한
글의 모든 문자를 구성하는 최소한의 도형들만을 추려내면 17개의 선과 1개의 도형 그리고 1개의 원이 필요하다.
모두 20개의 도형만으로 글자 구성 규칙을 도입하여 모든 한글을 만들 수 있게 된다.

이제 영어를 생각해 보자. 한글처럼 점으로부터 시작하는 기획을 생각할 때, 그나마 가장 구성하기 쉬운 방법이 대문자 표기일 것이다. 영어의 대문자를 나열하면 ‘ABCDEFGHIJKLMNOPQRSTUVWXYZ’가 되는데 글자 모양을 봐서도 알겠지만 대각선 및 곡선의 체계가 매우 복잡하다. 선이 일차방정식으로 표현 가능하다면 원은 x와 y값이 모두 이차인 만큼 그 복잡성이 더하다. 또한 선으로만 구성된 문자를 보더라도 기초 문자의 구성이 한글에 비해 매우 복잡하다. 문자를 구성하는 기초 체계가 없으니 글자 자체를 하나의 점들의 집합으로 구성해 암호화해서 컴퓨터에 인식시킬 수밖에 없는데 이럴 경우 역시 26가지 도형을 암호화해야 한다는 측면에서 한글의 20개와 비교해 비경제적이다. 하지만 여기서 끝이 아니다. 각자는 글자 구성 규칙을 적용해 단어 혹은 문장을 구성할 수 있을 것인데 우리는 앞에서 이미 한글이 영어에 비해 보다 정확하고 풍부한 음성을 표현함을 보았다. 기초 도형의 구성에서부터 문자의 사용까지 한글의 체계성, 경제성 그리고 실용성은 더 이상 영어에 비교할 바가 아닌 것 같다.
III. 과학적인 문자 한글
지금까지 ‘과학적’이라는 말의 의미에서부터 한글의 실용성 그리고 컴퓨터 프로그램에의 적용까지 한글의 과학성을 하나씩 살펴보았다. 이제 실제 현대의 학자들이 언급하는 한글의 과학성과 예찬 혹은 사용에 대한 몇 몇 사례를 통해서 한글의 과학성에 대한 근거를 제시하고 이 글을 마칠까 한다.
1. 조합형
필자가 앞장에서 임의로 구성한 한글 표현방식과 유사한 아이디어로 구성된 방식을 조합형이라고 한다. 조합형이란 한글의 초성과 같은 기본형 문자를 기초로 이들을 조합하여 글자를 구성하는 방식으로 ‘을’, ‘작’ 등의 완성된 글자를 하나하나 컴퓨터에 입력하여 사용하던 종전의 완성형 방식에 비해 매우 폭 넓은 표현력과 효율성을 자랑하는 방식이다. 현재 조합형은 문서 편집 프로그램의 대표적인 한글 표현 방식이며 이 방식 역시 훈민정음에 나온 한글의 기본원리를 따랐을 뿐임을 알 수 있다.
2. 조선일보 소개 사례
‘한글 세계화’를 주장하는 학자들은 한글의 무한한 개방적 구조에 주목한다. 김형배 한글문화연대 학술위원은 “한글은 초성 다섯 자(ㄱ, ㄴ, ㅁ, ㅅ, ㅇ)와 중성 세 자(·, ㅡ,ㅣ)를 바탕으로 가획의 원리에 의해 파생자를 만들었을 뿐 아니라 연서(連書·세로쓰기에서 자음을 위아래로 쓰는 것)나 병서(竝書·둘 이상의 자음이나 모음을 아울러 쓰는 것)에 의해 더 많은 글자를 만들 수 있다”며 “우리말에 없는 외국어 발음을 적기 위한 발음기호로 한글을 활용할 수 있는 근거가 바로 이것”이라고 설명했다. 김 위원은 “한글 창제 당시 지금은 없어진 4글자(?, ·, △, ?)와 중국어를 적기 위한 6자 등을 조합하면 무려 399억자를 만들 수 있다”며 “정인지가 훈민정음 해례 서문에서 ‘바람 소리, 학 울음소리, 닭 울음소리, 개 짖는 소리까지도 적을 수 있다’고 한 것은 결코 과장이 아니다”라고 주장했다.
한글의 가능성을 실제 상품으로 연결시킨 사례도 있다. 대표적 인물이 안마태(73) 신부. 그는 작년 6월 영어 알파벳으로 원하는 글자를 찾아오는 중국의 병음(倂音)식 프로세서를 대체할 수 있는 ‘안음(安音) 3.0’을 출시, 중국 현지에서 뜨거운 반응을 얻었다. ‘안음 3.0’은 한글을 발음기호로 이용해 중국어를 표기할 수 있는 프로그램. 예를 들어 ‘중화인민공화국(中華人民共和國)’을 병음법으로 표기하려면 ‘zhong hua ren min gong hua guo’와 같이 24개의 알파벳을 일일이 입력해야 한다. 그러나 ‘안음 3.0’을 이용하면 ‘쭝훠런민꿍훠궈’를 입력만 해도 화면에 해당 한자가 떠오른다. 동음이의어의 경우 획 수나 성조 등을 참조해 여러 개 중 하나를 선택할 수 있다. 현재 중국 동항에 거주하며 제품 상용화에 힘 쏟고 있는 그는 “영어나 일본어도 동일한 방식으로 한글을 입력용 발음 기호로 사용할 수 있으며 현재 관련 연구를 진행 중”이라고 밝혔다.
3. 한겨레 일보 사례 2003. 10. 08
“한글은 과학이다” 한글은 수학으로 분석할 수 있는 지구상의 유일한 문자이며, 슈퍼컴퓨터로도 풀기 힘든 암호문을 만드는 데 활용할 수 있는 과학적 문자라는 분석이 나왔다. 미국 앨라배마주립대의 김기항(68,·수학) 석좌교수는 지난 5년여 동안 이런 한글의 ‘과학성’을 분석한 논문을 잇따라 내며 이를 미국 학계와 교민사회에 널리 알려왔다. 한국한림원 종신회원이기도 한 그는 2001년 대한수학회 소식지에 ‘신기한 훈민정음의 수학적 특성’이란 논문을, 최근엔 ‘한글과 암호’라는 논문을 내는 등 한글 분석 연구를 계속하고 있다. 그는 전자우편 인터뷰를 통해 “24개 모든 자·모음은 수학의 대칭성으로 설명할 수 있다”며 “한글은 순열을 이용해 슈퍼컴퓨터로도 해독하는 데 수천년 걸릴 암호문을 만들 수 있다”고 말했다. 예컨대 점 ‘.’이 모여 수평선분 ‘ㅡ’와 수직선분 ‘ㅣ’을 이루고 이들의 조합인 ‘ㅗ’ ‘ㅛ’ 등을 이동·회전해 모든 모음을 얻을 수 있다. 자음들 역시 ‘ㅡ’와 ‘ㅣ’가 연결·이동하거나 회전해 ‘ㄴ’ ‘ㅂ’ 등을 만든다. 김 교수는 “영어나 아랍어에도 없는 수학적 구조를 한글만이 지녔다”며 “참으로 아름답고 신기한 문자”라고 평했다. 그는 “앨리배마주립대 미국인 학생들도 1시간 만에 한글 자·모음을 쉽게 깨쳤을 정도”라고 소개하며 순열을 이용한 한글 암호문 작성의 실례를 보이기도 했다.
4. 한글, 영어, 일어, 그리고 중국어 문자사용 비교
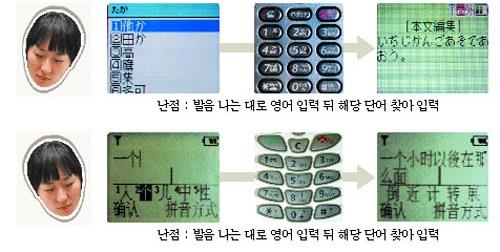
아래 그림은 한 네티즌이 자신의 블로그에 한글, 영어, 일본어, 중국어로 문자를 보내보고 불편한 점을 나타낸 그림이다. 기본적으로 ‘한 시간 뒤에 거기서 보자’와 같은 말을 전하는데 한글은 40타 이하 영어는 40타 이상의 키패드를 쳐야 한다고 한다.

위의 네 가지 사례 외에도 한글의 과학성과 실용성을 주장하는 사례는 무수히 많다. 그리고 이미 한글은 유네스코 지정 세계문화 유산으로 등재되어 있을 정도로 그 과학성이 인정받았다. 가장 큰 문제라면 한글을 가장 많이 쓰는 우리의 한국에 대한 무관심이랄까? 올해로 한글이 세계 공용어로 등재되었다고 한다. 세계화 시대에 외국어의 사용을 강조하는 것도 중요하겠지만 과학의 결정체인 한글의 우수성을 다시 한 번 상기하는 것 역시 매우 중요할 것이다.
참고문헌
김미경, 『대한민국 대표 브랜드 한글』, 자우출판사, 2006
김영욱, 「한글과 언어문화 강의노트」
정경일 외12명, 『한국어의 탐구와 이해』, 박이정, 2002
A.F. 차머스, 『과학이란 무엇인가?』, 서광사, 2003, 신중섭, 이상원 옮김
Hewings, M. & Goldstein, S., Pronunciation Plus, Cambridge university press.
Pyles, T. and Algeo, J, The Origins and Development of the English Language, Harcourt, 1992
'덕쥘' 카테고리의 다른 글
| 2030년의 인공지능과 삶(Artificial Intelligence and Life in 2030) (0) | 2023.06.27 |
|---|---|
| 글쓰기에 ChatGPT를 윤리적으로 사용하는 방법 (3) | 2023.06.17 |
| 한글의 우수성 (0) | 2020.03.03 |
| 니체가 옳았다? (0) | 2020.03.03 |
| 기계가 인간 보다 똑똑해 지면 무슨 일이 일어날까? (0) | 2020.01.21 |




댓글